MATEMÁTICA - ATIVIDADE 01 - INTRODUÇÃO ÀS FUNÇÕES - 2º BIMESTRE
Questão ❶
Considere os conjuntos \(A = \{ a, b, c\}\) e \(B = \{0, 2\}\). Determine \(A \times B\) e \(B \times A\).
Questão ❷
Considere o conjunto $A = { 0, 1, 2, 3, 4}$ e o conjunto $B = {1, 3, 5, 7, 9}$. A relação $A \to B$ é tal que $y = x + 2$. Complete o quadro com as informações pedidas:
| \(x\) | \(y = x + 2\) | É um par possível? |
|---|---|---|
| 0 | 2 | Não, porque \(2 \notin B\). |
| 1 | ||
| 2 | ||
| 3 | 5 | Sim, porque \(5 \in B\). |
| 4 |
Agora responda: A relação apresentada é função?
Questão ❸
Dada a função \(f(x) = -2x + 5\), responda:
a) Qual o valor de \(f(3)\)?
b) Qual é a imagem de 5?
c) Qual é o elemento cuja imagem é 15?
Questão ❹
Observe os diagramas de flechas a seguir:
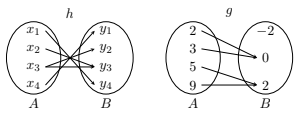
Algum deles indica função? Se algum diagrama não mostra função, explique o porquê.
❶ - \(A \times B = \{ (a, 0), (a, 2), (b, 0), (b, 2), (c, 0), (c, 2) \}, B \times A = \{ (0, a), (0, b), (0, c), (2, a), (2, b), (2, c) \}\). ❷ A relação não representa uma função, pois \(x = 2 \rightarrow y = 4\) e \(4 \notin B\). ❸ - a) \(f(3) = -1\) b) \(f(5) = -5\) c) \(y = 15 \rightarrow x = -5\). ❹ - O diagrama \(g\) é função, o diagrama \(h\) não, visto que há elemento de \(A\) que tem mais de uma ligação no conjunto \(B\).
