MATEMÁTICA - ATIVIDADE 03 - FUNÇÕES DE PRIMEIRO GRAU - 2º BIM
Questão ❶
Considere os seguintes pares de pontos e responda ao que se pede:
a) \((0, 1)\) e \((3, 7)\).
b) \((-1, -1)\) e \(3, 3)\).
c) \((-1, 1)\) e \((3, 3)\).
d) \((-1, 4)\) e \((2, 1)\).
Em cada item, considere a reta \(f(x) = ax + b\) e determine:
- O valor de Δy.
- O valor de Δx.
- O coeficiente a.
- O coeficiente b.
Questão ❷
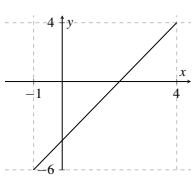
O gráfico a seguir mostra a função \(f(x) = ax + b\). Determine a fórmula da função. Sugestão: siga os passos do exercício anterior.
Questão ❸
O salário de um vendedor é composto por duas partes. A primeira, fixa, de R$ 920,00 mensais. A segunda, formada pela comissão, que depende do valor total x que ele consegue vender durante o mês. Essa comissão equivale a 2% do valor x. considerando este cenário, responda ao que se pede:
a) Qual é a comissão recebida pelo vendedor se o total em vendas durante um mês for de R$ 200,00?
b) Qual é a fórmula que dá o salário desse vendedor (y) em função do valor total de vendas (x)?
c) Considere as seguintes vendas realizadas pelo venvedor durante o mês de abril:
| Fila | Número de Assentos (Na fila) | Número de Assentos (Total) |
|---|---|---|
| 9 | 69 | 369 |
| 10 | 76 | 445 |
| 11 | 83 | 528 |
Calcule o salário desse vendedor caso ele não efetue mais vendas durante o mês.
Questão ❹
Desenhe o gráfico da função \(f(x) = -x +3\) no plano cartesiano a seguir.
Questão ❺
Desenhe o gráfico da função \(f(x) = \dfrac{x}{3} - 1\) no plano cartesiano a seguir.
❶ - a) \(\Delta y = 6, \Delta x = 3, a = 2, b = 1\) b) \(\Delta y = 4, \Delta x = 4, a = 1, b = 0\) c) \(\Delta y = 2, \Delta x = 4, a = \frac{1}{2}, b = \frac{3}{2}\) d) \(\Delta y = -3, \Delta x = 3, a = -1, b = 3\) ❷ - Do gráfico temos \(a = \dfrac{\Delta y}{\Delta x} = \dfrac{10}{5} = 2\). Com o valor de \(a\), podemos descobrir \(b\) para: \(4 = 8 + b \Rightarrow b = -4\), então, a fórmula é \(y = 2x - 4\). ❸ - a) R$ 4,00. b) \(y = 0,02x + 920\). c) O total de vendas foi de R$ 13 400,00, então, calculando 2% desse valor (R$ 268,00) e somando a R$ 920 temos o salário de R$ 1188,00. ❹ - 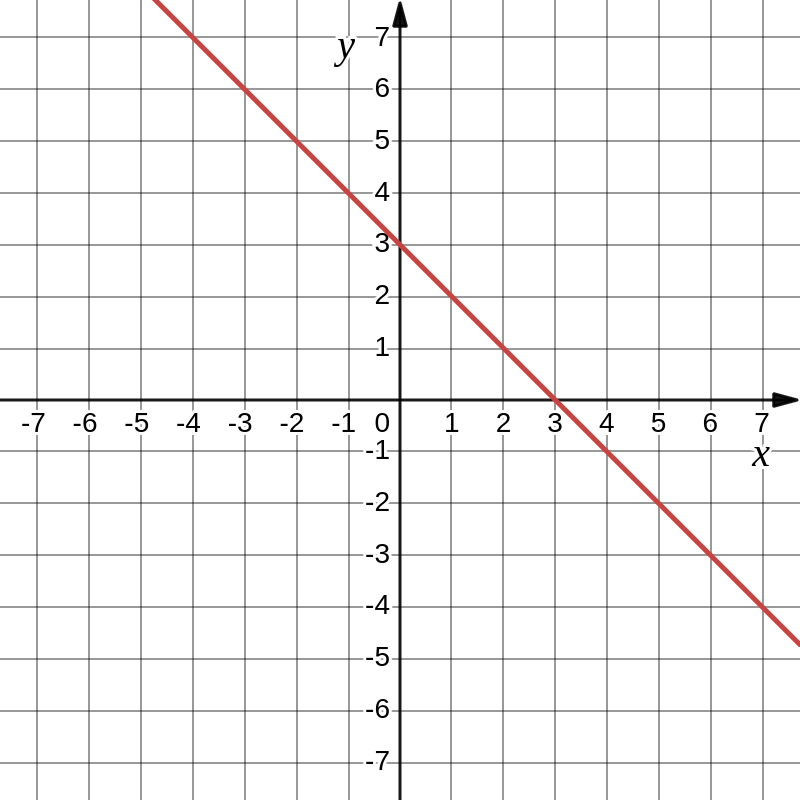 ❺ -
❺ -.png)
