APROVA MAT&FÍS - ATIVIDADE 01 - LEIS DE NEWTON E EQUAÇÕES DE 2º GRAU - 2º BIM
Matemática
Questão ➊
Observe as equações incompletas a seguir e resolva-as:
a) \(7x^{2} = 0\)
b) \(x^{2} - 5x = 0\)
c) \(x^{2} + 3x = 0\)
d) \(4x^{2} - 7x = 0\)
e) \(x^{2} - 9 = 0\)
f) \(x^{2} - 7 = 0\)
Questão ➋
Calcule o discriminante \(\Delta\) e depois resolva as equações completas:
a) \(x^{2} - 8x + 15 = 0\)
b) \(x^{2} + 5x + 6 = 0\)
Questão ➌
Utilize o discriminante \(\Delta\) para dizer se a equação \(x^{2} - 3x + 10 = 0\) admite soluções reais.
Física
Questão ➊
Um corpo com massa 200 g está posicionado sobre uma mesa. Duas forças, \(\overrightarrow{F}_{1}\) e \(\overrightarrow{F}_{2}\), de 70 N e 55 N, respectivamente, são aplicadas conforme o esquema:
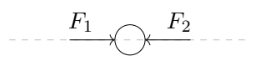
Determine a intensidade da força resultante desse sistema, além disso, determine sua direção e sentido.
➊ a) \(S = \{ 0 \}\) b) \(S = \{ 0, 5 \}\) c) \(S = \{ -3, 0 \}\) d) \(S = \{ 0, \frac{7}{4} \}\) e) \(S = \{ -3, +3 \}\) f) \(S = \{-\sqrt{7}, +\sqrt{7} \}\) ❷ a) \(\Delta = 4 \Rightarrow S = \{ 3, 5\}\) b) \(\Delta = 1 \Rightarrow S = \{ -3, -2 \}\) ❸ \(\Delta = -31\), então a equação não tem raízes reais.
❶ A força resultante será horizontal e para a direita, com intensidade de 15 N.
