APROVA MAT&FÍS - ATIVIDADE 02 - LEIS DE NEWTON E EQUAÇÕES DE 2º GRAU

Matemática

Questão ➊

A temperatura de um forno é, em centenas de graus Celsius, dada por:

\[ T(t) = -t^{2} + 6t\]

Com t medido em horas a partir do início do funcionamento do forno.

a) Em quanto tempo o forno atingirá a temperatura máxima?

b) Qual é essa temperatura?

Questão ➋

Um retângulo é tal que sua base mede \((100-x)\) e altura medindo x.

a) Qual é a função que dá a área desse retângulo?

b) Essa função admite valor de máximo ou valor de mínimo?

c) Qual é esse valor máximo/mínimo?

Física

Questão ➊

Considere a situação a seguir:

Um cavalo está atrelado a uma carroça e parado em relação ao solo. Se o cavalo puxar a carroça, na tentativa de colocá-la em movimento, ela também vai puxar o cavalo, com uma força de mesma intensidade, mesma direção e sentido contrário (ação e reação). Portanto, o conjunto não sai do lugar.

Isso está certo ou errado? Justifique.

Questão ❷

Três blocos, A, B e C, de massas iguais a 10,0, 3,0 e 7,0 kg, respectivamente, encontram-se em repouso sobre uma superfície horizontal. Uma força de intensidade 60 N é aplicada no bloco A, conforme mostra a figura. Despreze atritos e considere \(g = 10\) m/s².

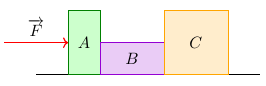
Faça o diagrama de forças correspondente ao sistema e determine a aceleração do sistema.