APROVA MAT&FÍS - ATIVIDADE 03 - REVISÃO A2

Questão 01

Uma criança brinca com uma varinha batendo na água de um lago em intervalos regulares e produzindo ondas. Suponha que em cada batida, uma única onda seja produzida. Se a criança diminuir o intervalo de tempo entre as batidas da varinha na água, as ondas produzidas passarão a ter:

Ⓐ Maior velocidade, mas mesma frequência.

Ⓑ Menor frequência, mas mesma velocidade.

Ⓒ Maior frequência, mas velocidade menor.

Ⓓ Menor comprimento de onda, mas mesma velocidade.

Questão 02

(ENEM) Em um dia de chuva muito forte, constatou-se uma goteira sobre o centro de uma piscina coberta, formando um padrão de ondas circulares. Nessa situação, observou-se que caíam duas gotas a cada segundo. A distância entre duas cristas consecutivas era de 25 cm e cada uma delas se aproximava da borda da piscina com velocidade de 1 m/s. Após algum tempo a chuva diminuiu e a goteira passou a cair uma vez por segundo. Com a diminuição da chuva, a distância entre as cristas e a velocidade de propagação da onda se tornaram, respectivamente,

Ⓐ Maior que 25 cm e maior que 1,0 m/s.

Ⓑ Maior que 25 cm e igual a 1,0 m/s.

Ⓒ Menor que 25 cm e menor que 1,0 m/s.

Ⓓ Menor que 25 cm e igual a 1,0 m/s.

Ⓔ Igual a 25 cm e igual a 1,0 m/s.

Questão 03

(VUNESP) Considere um lago onde a velocidade de propagação das ondas na superfície não dependa do comprimento de onda, mas apenas da profundidade. Essa relação pode ser dada por \(v = \sqrt{g \cdot d}\), em que \(g\) é a aceleração da gravidade e \(d\) é a profundidade. Duas regiões desse lago têm diferentes profundidades, como ilustrado na figura:

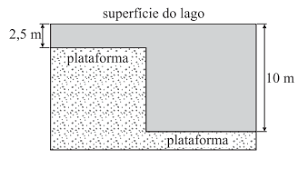
O fundo do lago é formado por extensas plataformas planas em dois níveis; um degrau separa uma região com 2,5 m de profundidade e a outra com 10 m de profundidade. Uma onda plana, com comprimento de onda \(\lambda\), forma-se na superfície da região rasa do lago e propaga-se para a direita, passando pelo desnível. Considerando que a onda em ambas as regiões possui a mesma frequência, pode-se dizer que o comprimento de onda na região mais profunda é:

Ⓐ \(\dfrac{\lambda}{2}\)

Ⓑ \(2\lambda\)

Ⓒ \(\lambda\)

Ⓓ \(\dfrac{3\lambda}{2}\)

Ⓔ \(\dfrac{2\lambda}{3}\)

Questão 04

Determinada onda se propaga inicialmente em um meio A, com velocidade \(v_{A}\) e frequência \(f_{A}\). Assim que entra em um meio B a sua velocidade de propagação passa a ser \(v_{B}\) e sua frequência \(f_{B}\). Neste caso, os comprimentos de onda nos meios A e B são, respectivamente, \(\lambda_{A}\) e \(\lambda_{B}\). Sabendo que a velocidade \(v_{B}\) é quatro vezes maior do que a velocidade \(v_{A}\), determine a relação entre:

a) As frequências \(f_{A}\) e \(f_{B}\).

b) Os comprimentos de onda \(\lambda_{A}\) e \(\lambda_{B}\).

Questão 05

Considere que ondas se propagam em uma piscina com duas profundidades. Na parte mais profunda, o comprimento da onda é dada por \(\lambda_{1} = 1\) m, enquanto na região mais rasa tem-se \(\lambda_{2} = 0,25\) m. Qual é a razão entre as velocidades dessas ondas?

Questão 06

Observe a onda a seguir:

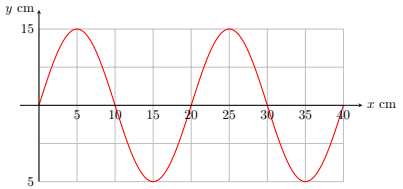
Com base na figura anterior, determine:

a) Qual é a amplitude da onda?

b) Qual é o comprimento da onda?

c) Considerando que a frequência é de 60 Hz, determine sua velocidade, em m/s.

Questão 07

Observe a onda a seguir:

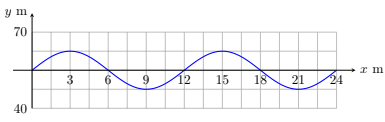
A partir do gráfico, determine:

a) A amplitude da onda.

b) O comprimento da onda.

c) Considerando que o período da onda é de 5 s, determine a frequência da onda, em Hz.

d) Qual é a velocidade da onda, em m/s?