MATEMÁTICA - ATIVIDADE 01 - FUNÇÕES EXPONENCIAIS
Questão ➊
Considere a função \(f(x) = 3^{x + 1} + 2\)$. Calcule:
a) \(f(-1)\)
b) \(f(2)\)
c) \(f(4)\)
Questão ➋
Observe a função a seguir que relaciona substâncias às suas meias-vidas:
\[ Q(t) = Q_{0} \cdot \left( \frac{1}{2} \right)^{\frac{t}{p}}\]
a) Identifique a parte da função que a caracteriza como exponencial.
b) Essa função é crescente ou decrescente? Justifique.
Questão ➌
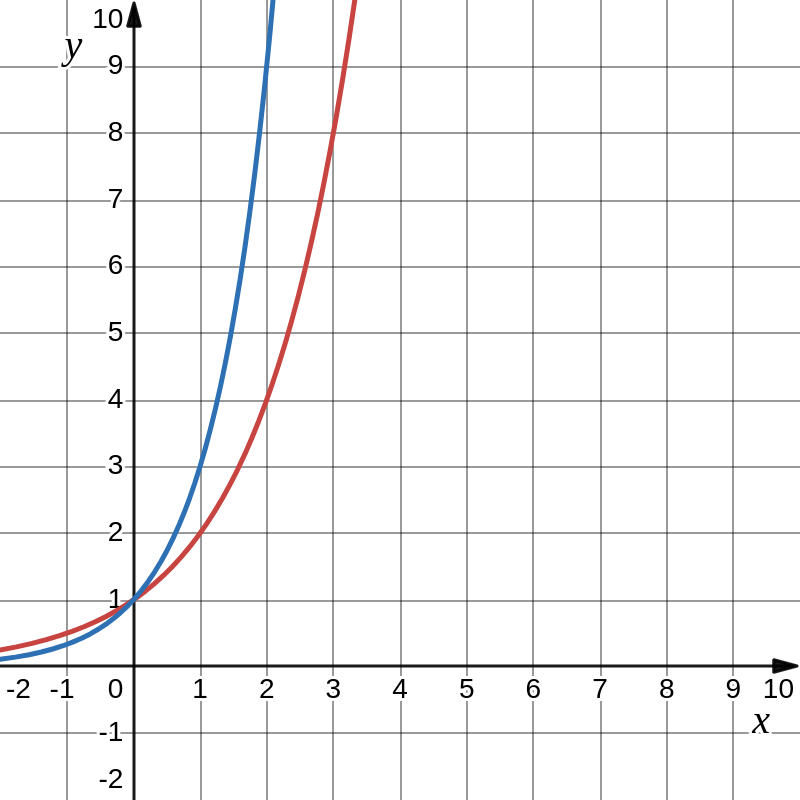
Considere as funções \(f(x) = 2^{x}\) e \(g(x) = 3^{x}\). Represente ambas no plano cartesiano a seguir:
➊ a) \(f(-1) = 3^{-1+1} + 2 = 3^{0} + 2 = 1 + 2 = 3\) b) \(f(2) = 3^{2+1} + 2 = 3^{3} + 2 = 27 + 2 = 29\) c) \(f(4) = 3^{4+1} + 2 = 3^{5} + 2 = 243 + 2 = 245\) ➋ a) A variável \(t\) estar no expoente de \(\dfrac{1}{2}\). b) Decrescente, pois a base do exponencial é um número real entre 0 e 1. ➌ \(f(x)\) em vermelho. \(g(x)\) em azul.